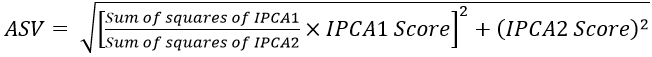Research Article
Volume 1 Issue 2 - 2019
Stability and Adaptability Analysis in Advance Fine Grain Rice (oryza sativa l.) Genotypes for Yield
1Rice Research Institute Kala shah Kaku, Punjab Pakistan
2Pakistan Agriculture Research Council, Rice Program, Kala Shah Kaku, Pakistan
3Ayub Agricultural Research Institute, Faisalabad, Pakistan
2Pakistan Agriculture Research Council, Rice Program, Kala Shah Kaku, Pakistan
3Ayub Agricultural Research Institute, Faisalabad, Pakistan
*Corresponding Author: Zulqarnain Haider, Rice Research Institute Kala shah Kaku, Punjab Pakistan.
Received: May 26, 2019; Published: September 12, 2019
Abstract
The analyses like Additive Main effect and Multiplicative Interaction (AMMI) and Genotypic & Genotypic-by-Environment (GGE) analysis are being used world-wide to interpret Multiple Environment Trial (MET) very successfully by many researchers especially plant breeders. Measurement of relevant performance of tested genotypes and their stability over a number of tested environments particularly in terms of their yields, is the key objective in the development of high yielding varieties and is an important goal in plant breeding programs. The objective of this study was to explore genotype × environment (G × E) interaction and its impact on rice yield stability. Eight (8) cultivars including one check variety (Basmati 515) were tested at five different agro-ecological sites. Combined analysis of variance clarifies that the G × E component was highly significant for rice paddy yield across various environments in Punjab Province, Pakistan. Thus, we proceeded with statistical analysis using AMMI and GGE biplot analyses to calculate the interactions and define their main effects, and calculated phenotypic stability. AMMI analysis of variance of paddy yield was highly significant and was affected by environments, genotypes and G × E interaction. The amount of G×E interaction sum of squares established that there were significant differences in genotypic responses across environments. First two Interaction Principal Components i.e. IPCA1 and IPCA2 combined had almost equivalent sum of squares to genotypes and contributed to 86.29% of the total GEI. Both of these principal component axes of interaction were also very highly significant (p < 0.001). AMMI analysis depicts that PK8680 (FV7) was the highest yielding genotype and the most stable among all the genotypes studied, after PK8667 (FV6) which showed higher yields after PK8680. Therefore, these two lines being higher yielder and stable can be used for general cultivation. Site Farooqabad was the most stable and most productive environment. PK8680 was among four highest yielders at all the studied locations, indicating that this line had both the characters of best performance and stability to be the best genotype. Results of AMMI further show that genotypes FV2, FV3, FV5, FV7 and FV8 performed better at locations E1 and E5. Other all genotypes were better performing at E2, E3 and E4 locations. GGE biplot also depicted the same results. AMMI and GGE analysis further divided genotypes and environments in two genotypic groups and mega-environments. It can be concluded that both AMMI and GGE analyses are equally helpful in assessing the Multi-Environment Trial (MET) data.
Keywords: AMMI; GGE; Varietal adaptation; Yield stability; G×E interaction; Rice (Oryza sativa L.)
Introduction
Yield stability is one of the key objectives in the development of plant varieties that have high yield potential combined with the better and wide adaptability over different ago-climatic conditions. Genotypes which yield better over different agro-climatic conditions are more adaptive and stable. On the other hand, genotypes which give more yield in a specific environment and less in another, are less stable in terms of yield and adaptive to only some specific environmental conditions. Comprehensive study of adaptability and stability of genotypes is an important goal in plant breeding programs (Das et al., 2011). This objective can be better understood and achieved by studying genotype × environment (GE) interaction impact on rice yield as it is one of the major source of variation. GE is major source of variation in traits such as yield which are governed by multiple genes to evaluate genotypes over multiple locations and can never be evaluated in a single environment. Thus, Genotype Environment Interaction (GEI) allows new lines to be assessed in Multi Environment Trials (MET). It also plays important role in determination of better suited breeding material that influences the selection process (Purchase et al., 2000; Haider et al, 2017). Regional adaptability yield trials provide the necessary platform to establish adaptation schemes and definition of cultivar commendation strategies (Gauch et al., 2008).
The adaptation strategies are focused on two goals i.e. to study the response of promising lines and to evolve the bases of varietal recommendation that involves the response of the tested genetic material in general (Mohebodini et al., 2012). When GEI can be predicted then these factors can be employed to tag specific genotypes to suitable environments (Crossa et al., 2002). Many statistical analysis techniques are present for these kind of experiments. These include parametric and non-parametric techniques that estimate the nature of GEI and their control (Rad et al., 2013). However, two most frequently used statistical techniques are the Additive Main effects and Multiplicative Interaction model (AMMI) and Genotype Main Effect G + G × E Interaction (GGE) model (Gauch et al., 2008).
To calculate the interactions and define their main effects, we normally apply combined analysis of variance. However, the analysis of variance alone does not partition the GEI. For the purpose of increasing accuracy and to study the genotype × environment interaction (GEI) the AMMI model is of primary choice. AMMI combines ANOVA with principal component analysis (PCA) (Sadeghi et al., 2011). It removes noise of interaction and adjusts the estimates of a given environment based on information from other environments. The main difference between AMMI and GGE biplot is that GGE biplot analysis is based on environment centered principal components analysis, whereas AMMI analysis is based on double centered principal components analysis. Both of these techniques are equally suitable and yield similar results (Haider et al, 2017; Yan et al., 2000; and Rad et al., 2013). GGE biplot analysis also helps us to quickly identify the group of locations with minimal crossover interactions specifically with the same highest yielding genotype (Rubio et al., 2004).
The present study aims to measure and interpret the Genotype × Environment Interaction (GEI) on yield performance and yield stability across different environment of rice lines. This may help to interpret varietal adaptability for rice yield that is a complex trait and to identify high yielding line in the respective test environments. The analyses like Additive Main effect and Multiplicative Interaction (AMMI) and Genotypic & Genotypic-by-Environment (GGE) analysis are being used world-wide to interpret Multiple Environment Trial (MET) very successfully by many researchers especially plant breeders. Measurement of relevant performance of tested genotypes and their stability over a number of tested environments particularly in terms of their yields, is the key objective in the development of high yielding varieties and is an important goal in plant breeding programs. Therefore, the objective of this study was also to explore genotype × environment (G × E) interaction and its impact on rice yield stability by using both these analyses and comparing their results keeping in view the requisite information needed by the rice breeders to study genotypes over different climates.
Material and Methods
Eight (08) high yielding rice lines with good cooking quality characters were evaluated for quantitative attributes in the stability performance and genotype environment interaction (GEI) studies along with one approved variety i.e. Basmati 515 as check during 2016. These nine cultivars were tested at five locations i.e. Kala Shah Kaku, Farooqabad, Gujranwala, Shoorkot and Faisalabad labeled as E1, E2, E3, E4 and E5 respectively (Table 1a). These locations are inside the core Basmati production area of Punjab Province, Pakistan. Shoorkot, Faisalabad, Farooqabad, and Kala Shah Kaku exhibit semi-arid environment while Gujranwala is moderately rain-fed area. Meteorological data of each target location/site is given in table 1b.
| Genotype Code | Genotype Name | Environment Code | Environment Name |
| FV1 | PK8892-11-2-1-1 | E1 | Kala Shah Kaku |
| FV2 | PK86117-11-1-1 | E2 | Farooqabad |
| FV3 | PK8431-1-2-1-2-4 | E3 | Gujranwala |
| FV4 | PK8430-1-2-1-3 | E4 | Shoorkot |
| FV5 | PK8431-6-1-1-1 | E5 | Faisalabad |
| FV6 | PK8667-8-5-1 | ||
| FV7 | PK8680-13-3-1 | ||
| FV8 | Basmati 515 (check) | ||
| FV9 | PK3810-30-1 |
Table 1a: The codes and names of rice genotypes and target environments.
| Kala Shah Kaku | Farooqabad | Gujranwala | Shoorkot | Faisalabad | ||
| Temperature °C | Max | 41.9 | 42.6 | 42.4 | 44.3 | 43.9 |
| Min | 34.0 | 34.7 | 34.4 | 35.7 | 36.3 | |
| Average | 37.9 | 38.4 | 38.1 | 39.9 | 39.9 | |
| Avg. Rainfall | Rain (mm) | 22.9 | 16.8 | 25.9 | 6.0 | 11.3 |
| Raindays | 12.3 | 10.6 | 12.6 | 6.4 | 8.1 | |
| Wind (km/h) | Max Wind | 16.2 | 15.9 | 16.1 | 20.2 | 15.4 |
| Av. Gust | 15.3 | 15.0 | 14.9 | 19.2 | 15.0 | |
| Av. Wind | 10.1 | 10.0 | 9.9 | 13.5 | 10.0 | |
| Avg. Pressure (mb) | 1001.4 | 1000.6 | 1001.7 | 1001.6 | 999.6 | |
| Humidity % | 27.7 | 25.9 | 28.0 | 22.6 | 24.0 | |
| Cloud % | 12.4 | 12.3 | 12.1 | 8.3 | 10.3 | |
Table 1b: Meteorological data (average) per month of each target location / site during crop growth period.
These genotypes were planted in plots of 2 x 6.25 m2 size with three replicates using Randomized Complete Block Design (RCBD). Fertilizer at the rate of 170:100:62 (N:P:K) kg/ha was applied. Zinc Sulphate was applied as per need basis. Data was recorded for several key contributing traits towards yield and in this study the yield is discussed. Analysis of variance, AMMI analysis and GGE Biplot analysis were performed using the VSNI GenStat software and confirmed by using SAS Statistics package.
The GGE biplot is a graphical representation of two parts of variation, genotypic and genotype × environment interaction (GEI), while it is constructed using the two most commonly used principal components i.e., PC1 and PC2. (Yan et al., 2000).
(i) The equation for AMMI model is as below:
Yij = μ + αi + βj + Σi=1k λn ξin njn + ρij + εij …………….. (1)
Yij = μ + αi + βj + Σi=1k λn ξin njn + ρij + εij …………….. (1)
Where Yij = Observed mean yield of genotype i in environment j.
μ = Grand mean
αi = Genotype main effect,
βj = Environmental main effect,
λn = Eigenvalues of the interaction IPCA,
ξinnjn = Genotype and environment scores for IPCA axis,
ρij = Interaction residual,
εij = Residual associated with genotype i in environment j.
μ = Grand mean
αi = Genotype main effect,
βj = Environmental main effect,
λn = Eigenvalues of the interaction IPCA,
ξinnjn = Genotype and environment scores for IPCA axis,
ρij = Interaction residual,
εij = Residual associated with genotype i in environment j.
Yield stability statistics were calculated according to Purchase et al. (2000) AMMI stability value (ASV) as under:
(ii) The equation for GGE biplot model is as under:
Yij = μ + βj + Σi=1k gil elj + εij ………………. (3)
Yij = μ + βj + Σi=1k gil elj + εij ………………. (3)
gil and elj are called PC1 scores for genotype i and environment j respectively.
Results and Discussion
Yield related traits of the studied genotypes are presented in table 2a. Plant height ranged from 115 cm to 149 cm, number of tillers were recorded 9 minimum and 15 as maximum tillers, panicle length was recorded with a short range from 29.48 to 31.78 cm. Maturity days were recorded in the range from 91 days to 103 days (days after transplanting) while the yield in tons per hectare was obtained ranging from 3.343 t/ha to 4.363 t/ha. This data represents the average values of these traits studied at all the target sites.
| Plant Height (cm) | Number of Tillers | Panicle Length (cm) | Maturity Days | Yield (t/ha) | |
| PK8892-4-2-1-1 | 128.7 | 15 | 29.90 | 98 | 4.260 |
| PK8647-11-1-1 | 119.4 | 10 | 29.48 | 103 | 3.343 |
| PK8431-1-2-1-2-4 | 127.5 | 9 | 30.50 | 94 | 4.068 |
| PK8430-1-2-1-3 | 115.8 | 11 | 31.40 | 91 | 4.363 |
| PK8667-8-5-1 | 149.9 | 9 | 31.78 | 101 | 3.785 |
| PK8667-8-5-1 | 141.9 | 11 | 30.65 | 94 | 4.083 |
| PK8680-13-3-1 | 117.0 | 11 | 29.63 | 94 | 4.363 |
| Basmati 515 (Check) | 134.6 | 12 | 29.93 | 97 | 4.123 |
| PK 3810-30-1 | 140.8 | 12 | 31.18 | 97 | 3.438 |
Table 2a: Average data of some yield related traits of studied genotypes at target locations.
(i) Combined Analysis of Variance
The Combined Analysis of Variance (CAV) given in Table 2b clarifies that the genotype × environment interaction (GEI) was highly significant (p < 0.001) for all the studied genotypes in terms of paddy yield across all studied environments. Thus, we proceeded with other statistical analysis including AMMI and GGE biplot analysis for calculating phenotypic stabilities and relative performances of genotypes along with their GEIs.
The Combined Analysis of Variance (CAV) given in Table 2b clarifies that the genotype × environment interaction (GEI) was highly significant (p < 0.001) for all the studied genotypes in terms of paddy yield across all studied environments. Thus, we proceeded with other statistical analysis including AMMI and GGE biplot analysis for calculating phenotypic stabilities and relative performances of genotypes along with their GEIs.
| Source of variation | df | SS | MS | F | F prob. |
| Replication (R) | 2 | 0.0351 | 0.0175 | 1.19 | |
| Environments (E) | 4 | 8.0775 | 2.0193 | 136.48 | <0.001 |
| Error (E×R) | 10 | 0.0722 | 0.0072 | ||
| Genotypes (G) | 8 | 13.301 | 1.6626 | 112.37 | <0.001 |
| GEI | 32 | 15.248 | 0.4765 | 32.21 | <0.001 |
| Error (E×R×G) | 88 | 1.3020 | 0.0148 | ||
| Total | 134 | 37.9654 |
Df = degrees of freedom; SS = Sum of Square; MS = Mean Square; F Probability of < 0.001 shows highly significant variation, Grand Mean = 3.9207, CV (E×R) = 2.17, CV(E×R×G) = 3.21
Table 2b: Combined analysis of variance of the productivity of rice trials and decomposition of the sum of squares of GEI.
Table 2b: Combined analysis of variance of the productivity of rice trials and decomposition of the sum of squares of GEI.
(ii) G×E Interpretation using AMMI analysis
The AMMI analysis of variance of paddy yield in tons per hectares (t ha-1) of nine rice genotypes tested in five environments is represented in Table 3. The analysis showed that paddy yield was highly significantly (p < 0.001) affected by environments (E), genotypes (G) and genotype × environment interaction (GEI). Out of the total sum of squares, 35.03% was attributed to genotypic effects and 21.27% was attributed to the environmental effects. The GEI provided 41.63% of the treatment sum of squares, while the replications effect was negligible.
The AMMI analysis of variance of paddy yield in tons per hectares (t ha-1) of nine rice genotypes tested in five environments is represented in Table 3. The analysis showed that paddy yield was highly significantly (p < 0.001) affected by environments (E), genotypes (G) and genotype × environment interaction (GEI). Out of the total sum of squares, 35.03% was attributed to genotypic effects and 21.27% was attributed to the environmental effects. The GEI provided 41.63% of the treatment sum of squares, while the replications effect was negligible.
| Source | df | SS | MS | F | p-value |
| Treatments (G+ E+ GEI) | 44 | 36.63 | 0.8325 | 52.65 | <0.001 |
| Genotypes (G) | 8 | 13.3 | 1.6627 | 105.15 | <0.001 |
| Environments (E) | 4 | 8.08 | 2.0194 | 279.69 | <0.001 |
| Blocks within environments (E) | 10 | 0.07 | 0.0072 | 0.46 | 0.91277 |
| G×E Interactions (GEI) | 32 | 15.25 | 0.4765 | 30.14 | <0.001 |
| IPCA1 | 11 | 11.16 | 1.015 | 64.19 | <0.001 |
| IPCA2 | 9 | 2 | 0.2227 | 14.09 | <0.001 |
| Residuals | 12 | 2.08 | 0.1733 | 10.96 | <0.001 |
| Pooled Error | 80 | 1.27 | 0.0158 | * | * |
| Total | 134 | 37.97 | 0.2833 | * | * |
IPCA = Interaction Principle Component Analysis, df = degrees of freedom; SS = Sum of Square; MS = Mean Square; F Probability of < 0.001 shows highly significant variation
Table 3: Analysis of variance table for AMMI model over environments
Table 3: Analysis of variance table for AMMI model over environments
Larger sum of squares (SS) for genotypes showed that the genotypes were largely dissimilar having significant differences among their yield means and resulted in the major variation in paddy yield. Whilst the environmental source of variation played 40% less role than genotypic variation. The extent of G×E interaction (GEI) sum of squares (SS) was almost two times greater than that of the genotypes, demonstrating that there were also significant differences in genotypic responses across environments.
Most accurate results for AMMI model can be obtained by using the first two IPCAs i.e., IPCA1 and IPCA2 (Yan and Rajcan, 2002). IPCA1 contributed 73.18% of the total GEI whereas the IPCA2 contributed 13.11% of the total GEI. Both the IPCA1 and IPCA2 combined had almost equivalent sum of squares to genotypes and contributed to 86.29% of the total GEI. Both of these principal component axes of interaction were also highly significant (p < 0.001) (Kebede A. and T. Tana, 2014). Therefore, for further simplicity and better understanding, AMMI2 model was the best model to predict the pattern of GEI.
| Genotype | Genotypic mean | IPCAg[1] | IPCAg[2] | Superiority | Mean Rank | Variances of ranks |
| FV1 | 4.200 | -0.25949 | 0.63367 | 0.05200 | 3.6 | 4.8 |
| FV2 | 3.326 | 0.32489 | -0.14221 | 0.42450 | 8.0 | 1.0 |
| FV3 | 3.934 | 0.82355 | -0.17569 | 0.17080 | 4.2 | 9.2 |
| FV4 | 4.156 | 0.47326 | 0.34195 | 0.06100 | 4.0 | 9.5 |
| FV5 | 3.760 | -0.33044 | -0.17209 | 0.17830 | 6.1 | 1.3 |
| FV6 | 4.066 | 0.07688 | 0.10129 | 0.07480 | 4.8 | 3.7 |
| FV7 | 4.292 | 0.08676 | -0.26888 | 0.02340 | 2.6 | 2.8 |
| FV8 | 4.070 | -0.50580 | -0.36532 | 0.09960 | 4.4 | 5.3 |
| FV9 | 3.482 | -0.68962 | 0.04729 | 0.35970 | 7.3 | 5.7 |
IPCAg = Interaction Principle Component Analysis for genotypes
Table 4: Genotype means, scores and stability coefficients for G×E data of paddy yield.
Table 4: Genotype means, scores and stability coefficients for G×E data of paddy yield.
Genotypic means depict the average yield of the genotypes over all the studied environments as indicated in table 4. Genotype FV2 (GM = 3.326) showed lowest value of genotypic mean while genotype FV7 (GM = 4.292) showed the highest value, followed by FV1, FV4, FV8 and FV6 with genotypic mean value of 4.200, 4.156, 4.070 and 4.066 respectively (Table 4).
The first interaction principal component i.e. IPCAg [1] values predicts the stability of the studied genotypes over the target environments. Higher the values, lowest the stability over variable environments and vice versa; regardless the positive or negative value. Table 4 shows that genotypes FV6 and FV7 had IPCAg [1] values close to zero, that is indicative of fact that these genotypes showed general adaptation to the environments under study. Genotype FV3 had the highest IPCAg [1] score that indicates its highest GE interaction and more productive specific environmental conditions. Among these genotypes, the FV6 has the lowest IPCAg [1] indicating lowest independent response thus proving to be most stable than any other line under varying environments, followed by FV7. Cultivars based on only these results may be selected for specific and broad adaptation (Mitrovic et al., 2012).
AMMI stability value quantifies and ranks genotypes according to their yield stability in varying environments. The Stability value is the distance from zero in a scatterplot of IPCA1 scores versus IPCA2 scores. IPCA1 scores contribute more to GE thus these are subjective to the relative difference between IPCA1 and IPCA2 scores. In AMMI stability value, a genotype with the lowest score is the most stable (Purchase et al., 2000). Here this measure is shown by superiority value of a genotype. Lowest superiority coupled with smaller mean rank, mean absolute difference of pair of ranks and variance of rank indicate best genotype that is high yielding and most stable. Such genotype can be recommended for a wide range of area. Among the lines under study, the genotype FV7 has the highest genotypic mean, lower IPCAg [1] and IPCAg [2] values meaning that it showed best yield performance, and proved to be more stable among a range of different environments thus can be preferably recommended for general production over a large area.
The IPCA scores of both genotypes and environments exhibit positive and negative values (Table 4 and Table 5). A genotype that has positive IPCA score in any environments may have negative interactions in other environments. Hence these scores are resultant of uneven genotypic response. (Bose et al., 2014). Among the studied environments/sites, E2 environment showed the highest value of environment mean value indicating its positive interaction with studied genotypes and the genotypes showed comparably higher paddy yield over this environment. Furthermore, Environment E2 also showed lowest IPCAe [1] value and hence was the most stable environment for all the cultivars and these genotypes performed equally well in this environment in terms of paddy yield. This inference is shown by Table 5 where it has the lowest IPCAe [1], lower environmental variance and highest environmental mean. However, it produced highest negative IPCAe [2] value higher independent negative response of genotypes across locations. Genotypic and environmental mean combination with IPCA scores of the similar sign produces positive specific interaction effect, while combination of contrary sign has negative specific interaction. Genotype FV4 performed best in E1 and E2 and thus it is suitable for these specific environments while genotype FV 7 performed best in E3, second best in E2, E4 and was fourth best in E1, E5 thus more suitable for general cultivation among all the environments. Environment E2 showed highest IPCAe [1] value thus indicating its instability for the genotypes.
| Environment | EM | IPCAe[1] | IPCAe[2] | EV | ES | Genotype Ranks | |||
| 1 | 2 | 3 | 4 | ||||||
| E1 | 3.954 | -0.98829 | 0.31330 | 0.3586 | 0.7269 | FV4 | FV3 | FV1 | FV7 |
| E2 | 4.370 | 0.23565 | -0.64123 | 0.1792 | 0.4420 | FV4 | FV7 | FV3 | FV6 |
| E3 | 3.730 | 0.44196 | 0.00401 | 0.2069 | 0.2356 | FV7 | FV3 | FV8 | FV4 |
| E4 | 3.867 | 0.72688 | 0.51946 | 0.3196 | -0.4162 | FV8 | FV7 | FV1 | FV6 |
| E5 | 3.682 | -0.41619 | -0.19554 | 0.0851 | -0.9883 | FV1 | FV8 | FV9 | FV7 |
EM = Environmental Mean, IPCAe = Interaction Principle Component Analysis for environments, EV = Environmental Variance, ES = Environmental Score
Table 5: Environment means, variances, scores and first four AMMI selections per environment.
Table 5: Environment means, variances, scores and first four AMMI selections per environment.
(iii) G×E Interpretation using GGE biplot analysis
In GGE biplot, the discussion focus will be on which won where pattern of genotypes, the mean genotypic performance and stability, and discrimination of genotypes in target environments. Environment focused scaling or principal component scaling is the most commonly used scaling method and explains the interrelationship among environments thus here it is also used. Data was not normalized because the units of data were same as also indicated by Yan et al. (2007). Figure 1 explains the GGE biplot with first two components i.e. PC1 and PC2 which represent 51.63% and 36.54% respectively making a total scatter plot of 88.17% of total GGE variance. With respect to close proximities of environments in scatter plot, environments can be grouped into two main mega environments where E2, E3 and E4 are in one mega environment and we name it mega environment-1. Mega environment-2 has environment E5 and E1. Multiple environments in one mega environment show similarity of environments.
In GGE biplot, the discussion focus will be on which won where pattern of genotypes, the mean genotypic performance and stability, and discrimination of genotypes in target environments. Environment focused scaling or principal component scaling is the most commonly used scaling method and explains the interrelationship among environments thus here it is also used. Data was not normalized because the units of data were same as also indicated by Yan et al. (2007). Figure 1 explains the GGE biplot with first two components i.e. PC1 and PC2 which represent 51.63% and 36.54% respectively making a total scatter plot of 88.17% of total GGE variance. With respect to close proximities of environments in scatter plot, environments can be grouped into two main mega environments where E2, E3 and E4 are in one mega environment and we name it mega environment-1. Mega environment-2 has environment E5 and E1. Multiple environments in one mega environment show similarity of environments.
The GGE biplot polygon is drawn joining the genotypes that are located farthermost from the biplot origin and all the other genotypes are contained within the polygon (convex hull). These farthermost genotypes have longest vectors in specific direction and measure their responsiveness to the environments and are also known as vertex genotypes. Here FV7, FV4, FV3, FV2, FV9, FV8 and FV1 are vertex cultivars and are most responsive to the environments while FV5 is less responsive to environments followed by FV6 that is least responsive to environments. Seven lines perpendicular to each side of the polygon are drawn that divides the convex hull into seven sectors. It is a general rule that the vertex genotype in all environments that share the same sector is the highest yielding genotype in it.
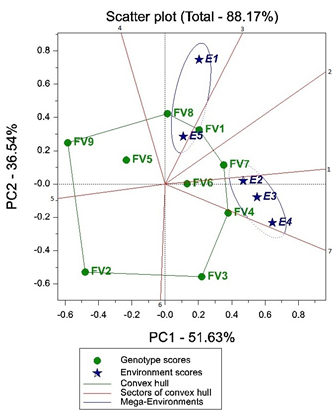
Figure 1: GGE biplot showing the performance of genotypes in different environments. Dotted mega environment lines indicate the extension of mega environment in another sector.
No three cultivars are on the same sector thus direct comparison among three cultivars is not possible for this type of convex hull. However, it is evident from the Figure 1 that FV7 performed better than FV4 in the mega environment-1. FV4 performed better than FV3 and in turn, FV3 performed better than FV6 that is not a vertex cultivar. FV7 performed better than FV1 in mega-environment-1 while in general FV1 performed better than FV7 in mega environment-2. Moreover, FV1 performed almost equal to the FV8 in mega environment-2. FV3 is better than FV2 in mega environment-1. FV9 and FV2 fell in sectors with no environment thus it means that these vertex cultivars were not the best in any of the environments. While in general FV9 performed better than FV2. FV9, FV2 and FV5 performed less in all the environments and among them FV2 performed the least for these given environments.
Figure 2 explains the test environment evaluation. Environment vectors connect environments to biplot origin. An acute angle between vectors signifies the positive correlation between environments i.e., E1 and E5. An obtuse angle between environments shows negative correlation i.e., E1 and E4 that has a slight obtuse angle, which indicates moderate crossover GE. A right angle between vectors show no correlation as in the case of E4 and E5 (Yan and Tinker 2006). The distance between vectors show dissimilarity among environments to discriminate cultivars thus here we have two distinct groups.
Length of the vectors for a particular environment is proportional to the standard deviation present with that environment and standard deviation within an environment is the measure of its discriminating ability. Here E1 and E4 are most discriminating and E5 is the least discriminating environment, and thus provide less information about cultivars within it. Hence, we can conclude that E5 can be safely dropped as a test environment. While, E1 and E4 can only be chosen to represent their respective groups because these are the ideal test environment and most discriminating. This may result in cost saving of experimentation (Yan and Tinker, 2006).
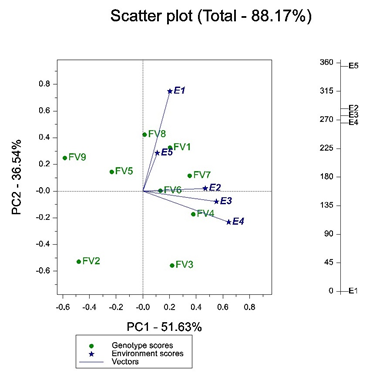
Figure 2: GGE Biplot relationship among environments for test environment evaluation. Data is not normalized, scaled for environment and genotypes and is environment centric.
Conclusion
Combined analysis of variance clarifies that the G × E component was highly significant (p < 0.001) for rice paddy yield across studied environments. AMMI analysis of variance of paddy yield was highly significant (p < 0.001) and was affected by environments, genotypes and G × E interaction. The amount of GEI sum of squares predicted that there were significant differences in genotypic responses across environments. First two Interaction Principal Components i.e. IPCA1 and IPCA2 combined had almost equivalent sum of squares to genotypes and contributed to 86.29% of the total GEI. Both of these principal component axes of interaction were also highly significant (p < 0.001). AMMI analysis depicts that PK8680 was the highest yielding genotype and the most stable among all the genotypes studied. PK8667 also showed higher yields after PK8680. Therefore, these two lines being higher yielder and stable can be used for general cultivation. Site Farooqabad was the most stable and most productive environment. PK8680 was among four highest yielders at all the studied locations, indicating that this line had both the characters of best performance and stability to be the best genotype. Results of AMMI further show that genotypes FV2, FV3, FV5, FV7 and FV8 performed better at locations E1 and E5. Other all genotypes were better performing at E2, E3 and E4 locations. GGE biplot also depicted the same results. AMMI and GGE analysis further divided genotypes and environments in two genotypic groups and mega-environments. It can be concluded that both AMMI and GGE analyses are equally helpful in assessing the Multi-Environment Trial (MET) data.
References
- Bose LK, NN Jambhulkar, K Pande, ON Singh. (2014). Use of AMMI and other stability statistics in the simultaneous selection of rice genotypes for yield and stability under direct-seeded conditions. Chilean Journal of Agriculture Research 74(1): 3-9.
- Chandrasiri GWJ, DSA beysiriwardena, BL Pieris, HMCK Jayathilake. (2002). Comparative evaluation of different statistical techniques on testing adaptability of rice varieties in varied environments. Sri Lanka Department of Agriculture 4: 1-13.
- Crossa J, PL Cornelius and W Yan (2002). Biplots of Linear-Bilinear Models for Studying Crossover Genotype Environment Interaction. Crop Scince 42: 619-633.
- Das S, RC Misra, MC Pattnaik, SK Sinha (2011). Integrated Analysis for Genotypic Adaptation in Rice. African Crop Science Journal 19(1): 15- 28.
- Gauch HG, HP Piepho, P Annicchiarico. (2008). Statistical analysis of yield trials by AMMI and GGE: Further considerations. Crop Science 48: 866–889.
- Haider Z, Akhter M, A Mahmood & Khan RAR (2017). Comparison of GGE biplot and AMMI analysis of multi-environment trial (MET) data to assess adaptability and stability of rice genotypes. African Journal of Agricultural Research 12(51): 3542-3548
- Kebede A and T Tana (2014). Genotype by Environment Interaction and Stability of Pod Yield of Elite Breeding Lines of Groundnut (Arachis hypogaea L.) in Eastern Ethiopia. Sci. Technol. Arts Research Journal 3(2): 43-46.
- Mitrovic B, D Stanisavljevi, S Treski, M Stojakovic, M Ivanovic, G Bekavac, M Rajkovic (2012). Evaluation of experimental maize hybrids tested in multi-location trials using AMMI and GGE biplot analysis. Turkish Journal of Field Crops 17(1): 35-40.
- Mohebodini M, R Karimizadeh, M Mohammadi, N Sabaghnia (2012). Principal coordinates analysis of genotype × environment interaction in grain yield of lentil genotypes. Agriculture Forestry Journal 57(11, 3): 93-107.
- Purchase JL, H Hatting, CS van Deventer (2000). Genotype × environment interaction of winter wheat (Triticum aestivum L.) in South Africa: Π. Stability analysis of yield performance. South African Journal of Plant & Soil 17: 101-107.
- Rad MRN, MA Kadir, MY Rafii, HZE Jaafar, MR Naghavi, F Ahmadi (2013). Genotype × environment interaction by AMMI and GGE biplot analysis in three consecutive generations of wheat (Triticum aestivum L.) under normal and drought stress conditions. Australian Journal of Crop Sciences 7(7): 956-961.
- Rubio J, JI Cubero, IM Martin, MJ Suso, F Flores (2004). Biplot analysis of trait relations of white lupin in Spain. Euphytica 135: 217-224.
- Sadeghi SM, H Samizadeh, E Amiriand M Ashouri (2011). Additive main effects and multiplicative interactions (AMMI) analysis of dry leaf yield in tobacco hybrids across environments. African Journal of Biotechnology 10(21): 4358-4364.
- Yan W, MS Kang, B Ma, S Woods, PL Cornelius (2007). GGE Biplot vs. AMMI Analysis of Genotype-by-Environment Data. Crop Science 47:641–653.
- Yan W and NA Tinker (2006). Biplot analysis of multi-environment trial data: Principles and applications. Canadian Journal of Plant Sciences 86: 623–645
- Yan W (2002). Single-value partitioning in biplot analysis of multi-environment trial data. Agronomy Journal 94: 990-996.
- Yan W, LA Hunt, P Johnson, G Stewart, X Lu (2002). On-farm strip trials vs. replicated performance trials forcultivar evaluation. Crop Science 42: 385-392.
- Yan W and I Rajcan (2002). Biplots analysis of the test sites andtrait relations of soybean in Ontario. Crop Science 42: 11-20.
- Yan W, LA Hunt, Q Sheng, Z Szlavnics (2000). Cultivar evaluation and mega environment investigation based on the GGE biplot. Crop Science 40: 597-605.
Citation: Rana Ahsan Raza Khan, Muhammad Ramzan, Zulqarnain Haider., et al. (2019). Stability and Adaptability Analysis in Advance Fine Grain Rice (oryza sativa l.) Genotypes for Yield. Journal of Agriculture and Aquaculture 1(2).
Copyright: © 2019 Zulqarnain Haider. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.