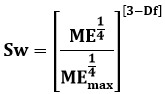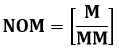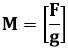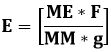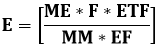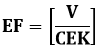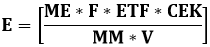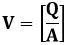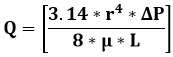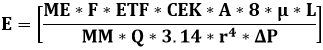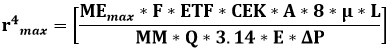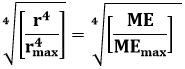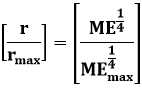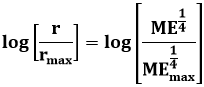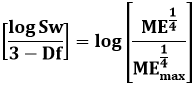Research Article
Volume 1 Issue 1 - 2019
Molar Enthalpy Fractal Dimension for Characterizing Shajara Reservoirs of the Permo-Carboniferous Shajara Formation
Department of Petroleum and Natural Gas Engineering, College of Engineering, King Saud University, Saudi Arabia
*Corresponding Author: Khalid Elyas Mohamed Elameen Alkhidir, Department of Petroleum and Natural Gas Engineering, College of Engineering, King Saud University, Saudi Arabia.
Received: May 15, 2019; Published: June 17, 2019
Abstract
The quality and assessment of a reservoir can be documented in details by the application of Molar enthalpy. This research aims to calculate fractal dimension from the relationship among Molar enthalpy, maximum Molar enthalpy and wetting phase saturation and to approve it by the fractal dimension derived from the relationship among capillary pressure and wetting phase saturation. Two equations for calculating the fractal dimensions have been employed. The first one describes the functional relationship between wetting phase saturation, Molar enthalpy, maximum Molar enthalpy and fractal dimension. The second equation implies to the wetting phase saturation as a function of capillary pressure and the fractal dimension. Two procedures for obtaining the fractal dimension have been utilized. The first procedure was done by plotting the logarithm of the ratio between Molar enthalpy and maximum Molar enthalpy versus logarithm wetting phase saturation. The slope of the first procedure = 3- Df (fractal dimension). The second procedure for obtaining the fractal dimension was determined by plotting the logarithm of capillary pressure versus the logarithm of wetting phase saturation. The slope of the second procedure = Df -3. On the basis of the obtained results of the fabricated stratigraphic column and the attained values of the fractal dimension, the sandstones of the Shajara reservoirs of the Shajara Formation were divided here into three units.
Keywords: Shajara Reservoirs; Shajara Formation; Molar enthalpy fractal dimension; Capillary pressure fractal dimension
Introduction
Seismo electric effects related to electro kinetic potential, dielectric permitivity, pressure gradient, fluid viscosity, and electric conductivty was first reported by Frenkel. Capillary pressure follows the scaling law at low wetting phase saturation was reported by Li and Williams. Seismo electric phenomenon by considering electro kinetic coupling coefficient as a function of effective charge density, permeability, fluid viscosity and electric conductivity was reported by Revil and Jardani. The magnitude of seismo electric current depends on porosity, pore size, zeta potential of the pore surfaces, and elastic properties of the matrix was investigated by Dukhin et al. The tangent of the ratio of converted electic field to pressure is approximately in inverse proportion to permeability was studied by Guan et al. Permeability inversion from seismoelectric log at low frequency was studied by Hu et al. They reported that, the tangent of the ratio among electric excitation intensity and pressure field is a function of porosity, fluid viscosity, frequency, tortuosity, fluid density and Dracy permeability. A decrease of seismo electric frequencies with increasing water content was reported by Borde et al. An increase of seismo electric transfer function with increasing water saturation was studied by Jardani and Revil. An increase of dynamic seismo electric transfer function with decreasing fluid conductivity was described by Holzhauer., et al. The amplitude of seismo electric signal increases with increasing permeability which means that the seismo electric effects are directly related to the permeability and can be used to study the permeability of the reservoir was illustrated by Ping., et al. Seismo electric coupling is frequency dependent and decreases expontialy when frequency increases was demonstrated by Djuraev., et al. An increase of permeability with increasing pressure head and bubble pressure fractal dimension was reported by Alkhidir. An increase of geometric relaxation time of induced polarization fractal dimension with permeability increasing and grain size was described by Alkhidir.
Materials and Methods
Sandstone samples were collected from the surface type section of the Permo-Carboniferous Shajara Formation, latitude 26° 52' 17.4", longitude 43° 36' 18". (Figure1). Porosity was measured on collected samples using mercury intrusion Porosimetry and permeability was derived from capillary pressure data. The purpose of this paper is to obtain Molar enthalpy fractal dimension and to confirm it by capillary pressure fractal dimension. The fractal dimension of the first procedure is determined from the positive slope of the plot of logarithm of the ratio of Molar enthalpy to maximum Molar enthalpy log (ME1/4/ME1/4max) versus log wetting phase saturation (logSw). Whereas the fractal dimension of the second procedure is determined from the negative slope of the plot of logarithm of log capillary pressure (log Pc) versus logarithm of wetting phase saturation (log Sw).
Where Sw the water saturation, ME the molar enthalpy in Joule/mole, MEmax the maximum molar enthalpy in Joule/mole, and Df the fractal dimension
Equation 1 can be proofed from
E=NOM*ME 2
E=NOM*ME 2
Where E the enthalpy in Joule, NOM number of moles, ME the molar enthalpy in Joule/mole
Where NOM the number of moles, M the mass in kilo gram, MM the molar mass in kilo gram/mole
Where M the mass in kilo gram, F the force in Newton, g the acceleration in meter/square second
Where g the acceleration in meter/square second, EF the electric filed in volt/meter, ETF the electric transfer function in volt * square second/square meter
Where EF the electric in volt/meter, V the velocity in meter/second, and CEK the electro kinetic coefficient in ampere/pascal *meter
Where V the velocity in meter/second, Q the flow rate in cubic meter/second, and A the area in square meter
Where Q the flow rate in cubic meter/second, r the pore radius in meter, ΔP the differential pressure in pascal, μ the fluid viscosity in pascal * second, L the capillary length in meter
Equation 24 the proof of equation 1 which relates the water saturation, molar enthalpy, maximum molar enthalpy and the fractal dimension
The capillary pressure can be scaled as
Sw=[Df-3]*Pc*constant 25
Sw=[Df-3]*Pc*constant 25
Where Sw the water saturation, Pc the capillary pressure and Df the fractal dimension.
Results and Discussion
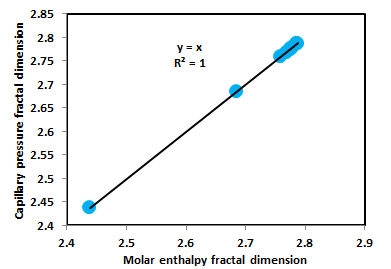
Based on field observation the Shajara Reservoirs of the Permo-Carboniferous Shajara Formation were divided here into three units as described in Figure 1. These units from bottom to top are: Lower Shajara Reservoir, Middle Shajara reservoir, and Upper Shajara Reservoir. Their attained results of the Molar enthalpy fractal dimension and capillary pressure fractal dimension are shown in Table 1. Based on the achieved results it was found that the Molar enthalpy fractal dimension is equal to the capillary pressure fractal dimension. The maximum value of the fractal dimension was found to be 2.7872 allocated to sample SJ13 from the Upper Shajara Reservoir as verified in Table 1. Whereas the minimum value of the fractal dimension 2.4379 was reported from sample SJ3 from the Lower Shajara reservoir as shown in Table 1. The Molar enthalpy fractal dimension and capillary pressure fractal dimension were detected to increase with increasing permeability as proofed in Table 1 owing to the possibility of having interconnected channels.
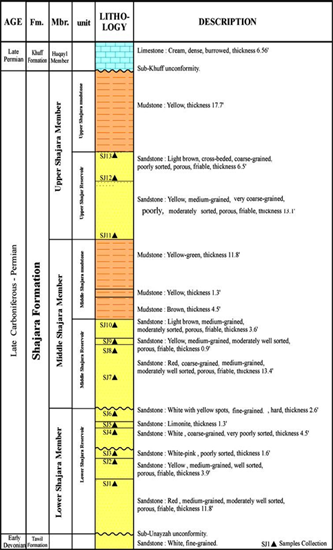
Figure 1: Surface type section of the Shajara Reservoirs of the Permo-Carboniferous Shajara Formation at latitude 26° 52' 17.4" longitude 43° 36' 18".
| Formation | Reservoir | Sample | Porosity % | K (md) | Positive slope of the first procedure Slope=3-Df | Negative slope of the second procedure Slope=Df-3 | Molar enthalpy fractal dimension | Capillary pressure fractal dimension |
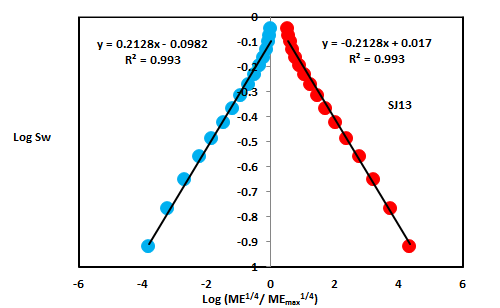
| Permo-Carboniferous Shajara Formation | Upper Shajara Reservoir | SJ13 | 25 | 973 | 0.2128 | -0.2128 | 2.7872 | 2.7872 |
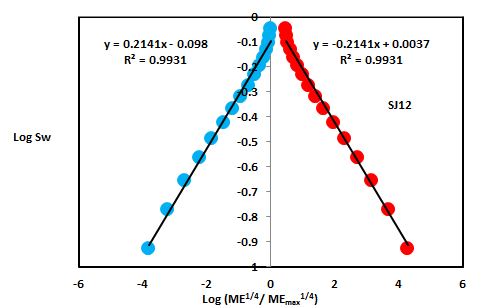
| SJ12 | 28 | 1440 | 0.2141 | -0.2141 | 2.7859 | 2.7859 | ||
| SJ11 | 36 | 1197 | 0.2414 | -0.2414 | 2.7586 | 2.7586 | ||
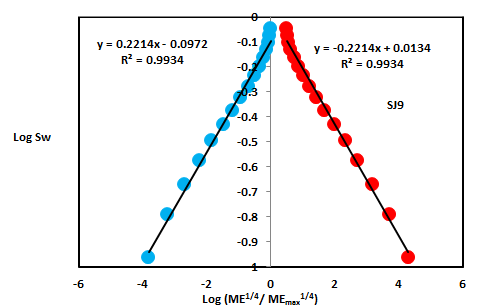
| Middle Shajara Reservoir | SJ9 | 31 | 1394 | 0.2214 | -0.2214 | 2.7786 | 2.7786 | |
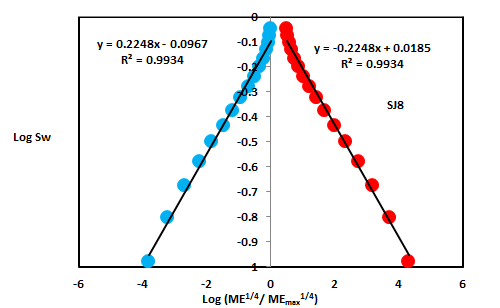
| SJ8 | 32 | 1344 | 0.2248 | -0.2248 | 2.7752 | 2.7752 | ||
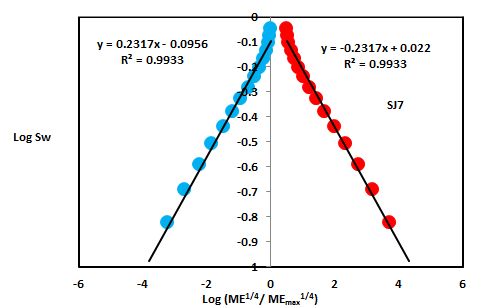
| SJ7 | 35 | 1472 | 0.2317 | -0.2317 | 2.7683 | 2.7683 | ||
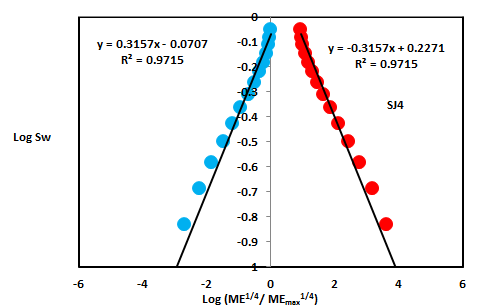
| Lower Shajara Reservoir | SJ4 | 30 | 176 | 0.3157 | -0.3157 | 2.6843 | 2.6843 | |
| SJ3 | 34 | 56 | 0.5621 | -0.5621 | 2.4379 | 2.4379 | ||
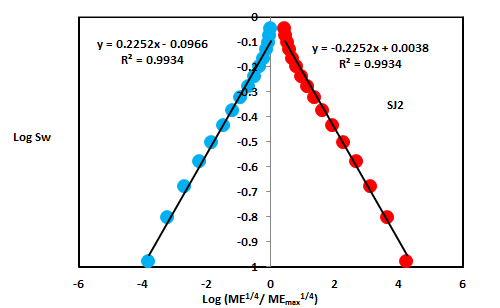
| SJ2 | 35 | 1955 | 0.2252 | -0.2252 | 2.7748 | 2.7748 | ||
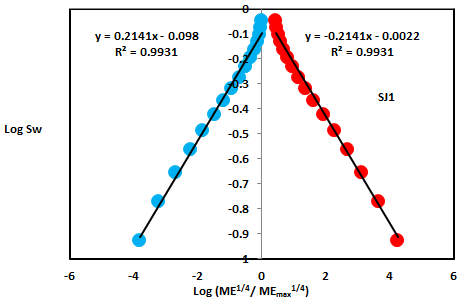
| SJ1 | 29 | 1680 | 0.2141 | -0.2141 | 2.7859 | 2.7859 |
Table 1: Petrophysical model showing the three Shajara Reservoir Units with their corresponding values of Molar enthalpy fractal dimension and capillary pressure fractal dimension.
The Lower Shajara reservoir was symbolized by six sandstone samples (Figure 1), four of which label as SJ1, SJ2, SJ3 and SJ4 were carefully chosen for capillary pressure measurement as proven in Table1. Their positive slopes of the first procedure log of the Molar enthalpy to maximum Molar enthalpy versus log wetting phase saturation (Sw) and negative slopes of the second procedure log capillary pressure (Pc) versus log wetting phase saturation (Sw) are clarified in Figure 2, Figure 3, Figure 4, Figure 5 and Table 1. Their Molar enthalpy fractal dimension and capillary pressure fractal dimension values are revealed in Table 1. As we proceed from sample SJ2 to SJ3 a pronounced reduction in permeability due to compaction was described from 1955 md to 56 md which reflects decrease in Molar enthalpy fractal dimension from 2.7748 to 2.4379 as quantified in table 1. Again, an increase in grain size and permeability was proved from sample SJ4 whose Molar enthalpy fractal dimension and capillary pressure fractal dimension was found to be 2.6843 as described in Table 1.
In contrast, the Middle Shajara reservoir which is separated from the Lower Shajara reservoir by an unconformity surface as revealed in Figure 1. It was nominated by four samples (Figure 1), three of which named as SJ7, SJ8, and SJ9 as illuminated in Table1 were chosen for capillary measurements as described in Table 1. Their positive slopes of the first procedure and negative slopes of the second procedure are shown in Figure 6, Figure 7 and Figure 8 and Table 1. Furthermore, their Molar enthalpy fractal dimensions and capillary pressure fractal dimensions show similarities as defined in Table 1.Their fractal dimensions are higher than those of samples SJ3 and SJ4 from the Lower Shajara Reservoir due to an increase in their permeability as explained in table 1.
On the other hand, the Upper Shajara reservoir was separated from the Middle Shajara reservoir by yellow green mudstone as shown in Figure 1. It is defined by three samples so called SJ11, SJ12, SJ13 as explained in Table 1. Their positive slopes of the first procedure and negative slopes of the second procedure are displayed in Figure 9, Figure 10 and Figure 11 and Table 1. Moreover, their Molar enthalpy fractal dimension and capillary pressure fractal dimension are also higher than those of sample SJ3 and SJ4 from the Lower Shajara Reservoir due to an increase in their permeability as simplified in table 1.
Overall a plot of positive slope of the first procedure versus negative slope of the second procedure as described in Figure 12 reveals three permeable zones of varying Petrophysical properties. These reservoir zones were also confirmed by plotting Molar enthalpy fractal dimension versus capillary pressure fractal dimension as described in Figure 13. Such variation in fractal dimension can account for heterogeneity which is a key parameter in reservoir quality assessment.
Conclusion
The sandstones of the Shajara Reservoirs of the permo-Carboniferous Shajara Formation were divided here into three units based on Molar enthalpy fractal dimension. The Units from base to top are: Lower Shajara Molar Enthalpy Fractal Dimension Unit, Middle Shajara Molar Enthalpy Fractal Dimension Unit, and Upper Shajara Molar Enthalpy Fractal Dimension Unit. These units were also proved by capillary pressure fractal dimension. The fractal dimension was found to increase with increasing grain size and permeability owing to possibility of having interconnected channels.
Acknowledgement
The author would to thank King Saud University, college of Engineering, Department of Petroleum and Natural Gas Engineering, Department of Chemical Engineering, Research Centre at College of Engineering, College of Science, Department of Geology, and King Abdullah Institute for research and Consulting Studies for their supports.
The author would to thank King Saud University, college of Engineering, Department of Petroleum and Natural Gas Engineering, Department of Chemical Engineering, Research Centre at College of Engineering, College of Science, Department of Geology, and King Abdullah Institute for research and Consulting Studies for their supports.
References
- Frenkel, J. (1944). On the theory of seismic and seismoelectric phenomena in a moist soil. Journal of physics 3(4). 230-241.
- Li, K., and Williams, W. (2007). Determination of capillary pressure function from resistivity data. Transport in Porous Media 67(1):1-15.
- Revil, A., and Jardani A. (2010). Seismoelectric response of heavy oil reservoirs: theory and numerical modelling. Geophysical Journal International 180(2). 781-797.
- Dukhin, A., Goetz, P., and Thommes, M. (2010). Seismoelectric effect: a non-isochoric streaming current.1 Experiment. Journal of Colloid and Interface Science 345(2). 547-553.
- Guan, W., Hu, H., and Wang, Z. (2012). Permeability inversion from low-frequency seismoelectric logs in fluid- saturated porous formations. Geophysical Prospecting 61(1). 120-133.
- Hu, H., Guan, W., and Zhao, W. (2012). Theoretical studies of permeability inversion from seismoelectric logs. Geophysical Research Abstracts 14 (2012): EGU2012-6725-1 2012 EGU General Assembly 2012.
- Borde C., S´en´echal P, Barri`ere J. et al. (2015). Impact of water saturation on seismoelectric transfer functions: a laboratory study of co-seismic phenomenon. Geophysical Journal International 200(3). 1317-1335.
- Jardani A., and Revil A. (2015). Seismoelectric couplings in a poroelastic material containing two immiscible fluid phases. Geophysical Journal International 202(2). 850-870.
- Holzhauer, J. Brito,D., Bordes,C. et al. (2016). Experimental quantification of the seismoelectric transfer function and its dependence on conductivity and saturation in loose sand. Geophysical Prospecting 65(4).1097-1120.
- Ping, R., Wei, J-X., Di, B-R. et al. (2016). Experimental research on seismoelectric effects in sandstone. Applied Geophysics 13(3): 425-436.
- Djuraev, U., Jufar, S.R., and Vasant. P. (2017). Numerical Study of frequency-dependent seismo electric coupling in partially-saturated porous media. MATEC Web of Conferences 87, 02001 (2017).
- Alkhidir KEME. (2017). Pressure head fractal dimension for characterizing Shajara Reservoirs of the Shajara Formation of the Permo-Carboniferous Unayzah Group, Saudi Arabia. Archives of Petroleum and Environmental Biotechnology 2.1-7.
- Al-Khidir KE. (2018). On Similarity of Pressure Head and Bubble Pressure Fractal Dimensions for Characterizing Permo-Carboniferous Shajara Formation, Saudi Arabia. Journal of Industrial Pollution and Toxicity 1(1). 1-10.
- Alkhidir KEME. (2018). Geometric relaxation time of induced polarization fractal dimension for characterizing Shajara Reservoirs of the Shajara Formation of the Permo-Carboniferous Unayzah Group, Saudi Arabia. Scifed Journal of Petroleum 2(1). 1-6.
- Alkhidir KEME. (2018). Geometric relaxation time of induced polarization fractal dimension for characterizing Shajara Reservoirs of the Shajara formation of the Permo-Carboniferous Unayzah Group-Permo. International Journal of Petrochemistry and Research 2(1). 105-108.
Citation: Khalid Elyas Mohamed Elameen Alkhidir. (2019). Molar Enthalpy Fractal Dimension for Characterizing Shajara Reservoirs of the Permo-Carboniferous Shajara Formation. Journal of Agriculture and Aquaculture 1(1).
Copyright: © 2019 Khalid Elyas Mohamed Elameen Alkhidir. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.