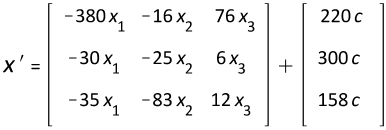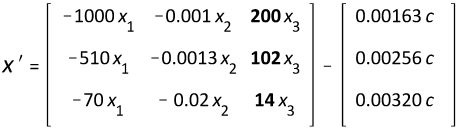Research Article
Volume 2 Issue 3 - 2020
The Autonomic Nervous System Fights Cancer in Mammals and Birds
M.D. Skolemarken 32, Broballe, 6430 Nordborg, Denmark
*Corresponding Author: Ebbe Lundsgaard, M.D. Skolemarken 32, Broballe, 6430 Nordborg, Denmark.
Email id: ebl@pc.dk
Email id: ebl@pc.dk
Received: August 04, 2020; Published: August 12, 2020
Abstract
Ten mammals and one bird were statistically evaluated, revealing a correlation between the independent variable, cancer risk, and the dependent variables, body weight and the brain-body weight ratio. This was treated in a system of nonhomogeneous differential equations, which graphically show the inclination for said variables and, moreover, the extent of sympathetic activity.
Budgerigars have half the cancer risk of mice, and big mammals are the least susceptible to cancer, possibly because a larger section of their brains is occupied by autonomous centers. These centers, which receive autonomous afferent nerves, are believed to perceive transformed cells that have lost the anchorage to adjacent cells and generated an excess of surface adrenoceptors. This triggers a cascade in the brain, causing extensive noradrenaline discharge from efferent sympathetic fibers in the vicinity of the receptive cell that terminates.
Keywords: Cancer-risk; Sympathicus; Noradrenaline; Autonomic-nervous-system; Brain; Body-weight.
Introduction
In accordance with the present statistics on ten mammals and one bird, the risk of cancer appears to decrease significantly with increasing number of cells, synonymous with body weight. Therefore, since the suppressor genes are largely evolutionarily immutable [1], the assumption of a cellular cancer defence challenges the laws of probability, which state that the cancer risk must increase with the number of cells.
The aim is to demonstrate that a systemic factor, the autonomic nervous system (ANS), which has the ability to innervate tumours [2] [3] and eradicate leukemia, lymphomas, and myelomas [4], is the primary defence against malignant cancer in mammals and birds [5].
In addition, ANS enables a connection between psyche and cancer and is considered independent of the will.
I argue that autonomous afferent fibers can perceive cancerous cells that lost the anchorage to adjacent cells and induce a hierarchical cascade in the brain. This may regulate the selective discharge of high levels of noradrenaline from sympathetic efferent fibers in the vicinity of the cancer cell, which is the obvious target due to its overexpression of adrenoceptors [6].
The discharge may occur in a pulse-like manner, probably with enhanced uptake of catecholamines from the surrounding interstitium to the nerve terminals, thereby increasing the synthesis of cAMP [7] in the cancer cell and accelerating cellular processes, leading to depletion of substrates and energy resources.
It is a discrete systemic factor, divergent from the hematogenous flow of catecholamines produced in the adrenal medulla, and it is located in the brain as verified by the following: Catecholamines in the brain are released by amphetamine, whose therapeutic activity predominantly takes place in the central nervous system (CNS). The application of amphetamine reduces the incidence of spontaneous tumours in mice and rats [8], however, not exclusively within the therapeutic CNS-area but throughout the entire body.
The low cancer risk in birds [9] may be attributed to a superior function of ANS since corpus striatum [10], a basic part of the cerebral hemispheres, is proportionally larger in birds and better developed, which favours instinctive behaviour and autonomous processes
Individual susceptibility
ANS acts as a mentally based cancer preparedness of variable strength formed early in life by conditioning. This explains why a particular carcinogen does not necessarily cause cancer in all exposed persons, which is analogous to the limited penetrance of some hereditary cancers.
ANS acts as a mentally based cancer preparedness of variable strength formed early in life by conditioning. This explains why a particular carcinogen does not necessarily cause cancer in all exposed persons, which is analogous to the limited penetrance of some hereditary cancers.
Mental conditions may be one of the reasons why
Denmark has one of the highest cancer rates in the world, despite huge investments in cancer research and extensive restrictions on suspected carcinogens. If so, less focus should be placed on the favourite of cancer research, carcinogens, in favour of cancer being related to passiveness and resignation due to an overprotective and controlling welfare society.
Denmark has one of the highest cancer rates in the world, despite huge investments in cancer research and extensive restrictions on suspected carcinogens. If so, less focus should be placed on the favourite of cancer research, carcinogens, in favour of cancer being related to passiveness and resignation due to an overprotective and controlling welfare society.
Materials
Table 1
The frequency of malignant tumours is either given in advance or was determined using the tables in the references [19] and [20] for rats and mice.
The elephant’s cancer mortality is 4.81% [21] against 11% in humans. Therefore, 4.81/11 multiplied by 320/105 (the tumour frequency in humans) yields 139.9/105, which equals the tumour frequency of elephants. It has been alleged that the elephant's low cancer risk is due to multiple copies of the p53 gene. However, the weight and cancer frequency of elephants persuasively match the tendency of the other species in the table, except the cat that deviates from this tendency, perhaps because of its independence.
The arbitrary unit, s, in table 1, elaborated in ‘Modelling’, estimates the strength of sympathicus. To prevent an incorrect downward slope of the brain/body line (figure 3), at least one s in a series of three must have a slightly different value, but this does not change the tendency of the lines for body weight and sympathicus.
Besides the reference [22], allometric formulas are used to calculate the brain-weight, and all weights are calculated in grams:
log (brain weight) = log 0.809096 + 0.525 log (body weight).
For rabbits, rats, and mice, a modified formula applies:
Log (brain weight) = log 0.0626 + 0.7739 log (body weight).
log (brain weight) = log 0.809096 + 0.525 log (body weight).
For rabbits, rats, and mice, a modified formula applies:
Log (brain weight) = log 0.0626 + 0.7739 log (body weight).
Methods
Body weight versus cancer
The configuration of the eleven body weights against their respective cancer frequencies was calculated in EXCEL and forms a hyperbola due to the potentiated increase in cancer of small species, which precludes a linear regression. However, the power regression, y = bxa, identical to y = 0.0391x−0.4709, is capable of handling this particular configuration, which exhibits strong bonds between body weight and the corresponding frequency of cancer.
The configuration of the eleven body weights against their respective cancer frequencies was calculated in EXCEL and forms a hyperbola due to the potentiated increase in cancer of small species, which precludes a linear regression. However, the power regression, y = bxa, identical to y = 0.0391x−0.4709, is capable of handling this particular configuration, which exhibits strong bonds between body weight and the corresponding frequency of cancer.
The raw data of the eleven species provide the correlation coefficient, r = 0.923147. Significance:
t = r [(n – 2) / (1 – r2)]1/2 = 7.203688.
t = r [(n – 2) / (1 – r2)]1/2 = 7.203688.
The degrees of freedom, n–2 = 11–2, which according to statistic tables yield: P <0.001.
Weight-ratio brain/body versus cancer
The Power regression, y = bxa = 2.5448x1.0451, from the raw data of the weight-ratio brain/body against the frequency of cancer in the eleven species yields, r = 0.800187, t = 4.002603, leading to: 0.001< P <0.01.
Modelling
Body weight, w, is equivalent to the number of cells, and the laws of probability state that the number of cells and the likelihood of occurrence of a malignant cell, C, will increase concomitantly. Paradoxically, a decrease in the cancer frequency is seen as w increases, which argues for the insertion of a compensatory factor, taking into account the immutable nature of the suppressor genes. However, this 'paradox' vanishes in favour of ANS whose trophic centres in the brain are phylogenetically adapted to the size and physiology of the species. Therefore, as the ratio between total brain weight and increasing body weight typically decreases in the species shown in table 1, the brain's ANS will in a potentiated manner constitute a growing proportion of the whole brain simultaneous with increasing body weight. This dynamic relationship means that ANS is progressively strengthened against interference from other brain structures as described in 'Discussion'.
Body weight, w, is equivalent to the number of cells, and the laws of probability state that the number of cells and the likelihood of occurrence of a malignant cell, C, will increase concomitantly. Paradoxically, a decrease in the cancer frequency is seen as w increases, which argues for the insertion of a compensatory factor, taking into account the immutable nature of the suppressor genes. However, this 'paradox' vanishes in favour of ANS whose trophic centres in the brain are phylogenetically adapted to the size and physiology of the species. Therefore, as the ratio between total brain weight and increasing body weight typically decreases in the species shown in table 1, the brain's ANS will in a potentiated manner constitute a growing proportion of the whole brain simultaneous with increasing body weight. This dynamic relationship means that ANS is progressively strengthened against interference from other brain structures as described in 'Discussion'.
Consequently, the body weight, not the brain, must be multiplied by an arbitrary 'sympathetic coefficient', s, which results in sw. This term is subtracted from the above theoretical cancer incidence and provides the observed cancer incidence, C – sw = c, or C = sw + c, where c qualifies for the independent variable.
Proportionality between w + b/w and sw + c
The function of w is the brain/body weight ratio, b/w. Their sum, w + b/w, is, as follows, very strongly correlated with sw + c.
The raw data of budgerigars and the ten mammals are inserted into w + b/w against sw + c and evaluated by linear regression, y = a + bx, identical to y = – 5.6714 + 0.334x. The coefficients, s, are set according to the table 1-values, whereby the resulting r2 = 0.999 delivers a convincing correlation.
The function of w is the brain/body weight ratio, b/w. Their sum, w + b/w, is, as follows, very strongly correlated with sw + c.
The raw data of budgerigars and the ten mammals are inserted into w + b/w against sw + c and evaluated by linear regression, y = a + bx, identical to y = – 5.6714 + 0.334x. The coefficients, s, are set according to the table 1-values, whereby the resulting r2 = 0.999 delivers a convincing correlation.
Because of the convincing correlation, the following terms are proportional:
w + b/w ∝ sw + c
w + b/w ∝ sw + c
This is converted to ordinary equations by inserting the dependent variables, x1, x2, and x3:
wx1 + (b/w)x2 = (sw)x3 + c
wx1 + (b/w)x2 = (sw)x3 + c
Subsequently, a regrouping is done to set up the nonhomogeneous differential equations in MAPLE:
diff (x (c), c) ± c = – wx1 – (b/w)x2 + (sw)x3.
diff (x (c), c) ± c = – wx1 – (b/w)x2 + (sw)x3.
Differential equations
The number of spontaneous tumours occurring in Sprague-Dawley rats is less than that observed in B6C3F1 mice, whereas some varieties exist in other strains of rats and mice.
The data of budgerigars (Melopsittacus) are uniquely defined, but they have an extremely high frequency of spontaneous, malignant tumours compared to other birds [18]. However, the frequency is only about one half of the tumours found in mice.
| Body weight | Brain/Body | Sympathicus | Cancer | |
| Sprague-Dawley Rats | – 0.380x1 | – 0.0163x2 | s0.380x3 | 0.220c |
| B6C3F1 Mice | – 0.030x1 | – (1/40)x2 | s0.030x3 | 0.300c |
| Budgerigars | – 0.035x1 | – (1/12)x2 | s10.035x3 | 0.158c |
Table 2
All values of table 2 are multiplied by 1000 and inserted into the matrices below.
The coefficient, s, of rats and mice is set to 1/5 body weight. The coefficient of budgerigars, s1, is set to 1/3 body weight in accordance with the advanced sympathetic activity.
The coefficient, s, of rats and mice is set to 1/5 body weight. The coefficient of budgerigars, s1, is set to 1/3 body weight in accordance with the advanced sympathetic activity.
Results
The computations for the construction of the following graphs, where s = [1/5 1/5 1/3]T, and − c is inserted into 'diff (x (c), c) ± c':
By setting the independent variable c equal to zero, the symbolically resolved coefficients, C1, C2, and C3, can be evaluated by aid of usual equations:
{C1 = 0.2546, C2 = 0.00138, C3 = -5.4518}.
{C1 = 0.2546, C2 = 0.00138, C3 = -5.4518}.
For rats, budgerigars and mice, the increase in cancer risk corresponds to a decrease in body weight and especially sympathetic activity offset by an increase in the brain to body. The juxtaposition of the elephant is legitimate as this configuration is also shown below.
Supplementary results
Additionally, the lines for whales, horses, and humans became computed. According to table 1 and ‘Modelling’, the sympathetic coefficients are set to [1/3 1/4 1/5]T, and + c in 'diff (x (c), c) ± c' prevents an inverted image around the abscissa, probably due to the large differences between the values.
[Whales horses humans]T
Additionally, the lines for whales, horses, and humans became computed. According to table 1 and ‘Modelling’, the sympathetic coefficients are set to [1/3 1/4 1/5]T, and + c in 'diff (x (c), c) ± c' prevents an inverted image around the abscissa, probably due to the large differences between the values.
[Whales horses humans]T
The symbolically resolved coefficients, C1, C2, and C3, approximate zero, so the 'boundary values', all with the value zero, are instead used for a numerical solution in MAPLE. The configuration for horses, dogs, and rabbits, [1/4 1/5 1/5]T, was constructed but not shown because it is similar to figure 2.
The crucial relationship between body weight and sympathicus versus cancer risk in beluga whales, horses, and humans is maintained as is the case in horses, dogs, and rabbits, but the latter group is not depicted. This also applies to the brain/body line, which, however, shows a greater increase in these groups.
As mentioned in ‘Materials’, at least one in three s must have a different value as the factual increase in brain-body ratio upon decreasing body weight will otherwise face downward. For example, s is equal to [1/5 1/5 1/5]T in the equations below, yielding a fraction of w that results in Gaussian elimination. The other values are identical to the previous matrices. [whales horses humans]T
The lines are symbolically resolved: {C1 = 8.93456,
C2 = 1.01801, C3 = 356.98061}.
Obviously, the brain/body line decreases when the three s are equal, [s s s]T, whereas the lines for body weight and sympathicus largely retain their positions and inclinations. This also applies to figure 1 and to the lines for horses, dogs, and rabbits.
C2 = 1.01801, C3 = 356.98061}.
Obviously, the brain/body line decreases when the three s are equal, [s s s]T, whereas the lines for body weight and sympathicus largely retain their positions and inclinations. This also applies to figure 1 and to the lines for horses, dogs, and rabbits.
Discussion
The figures were established using mathematics because the performance or magnitude of ANS in different species can hardly be determined experimentally. They show that the reduction in sympathetic activity is compatible with increasing cancer risk.
It has been disputed that cancer frequency is inversely related to body weight, but unfortunately such statistics are habitually adapted to the belief that genes are the decisive factor in the cancer defence. In contrast, the current statistics are unbiased, which, by virtue of a high level of significance, can be treated in a system of differential equations.
Cancer cells are not strictly autonomous as their numerous surface adrenoceptors require a balanced supply of noradrenaline to enable proliferation and migration of the transformed cell [23].
However, the transformed cell is wiped out by intensified sympathetic discharge of noradrenaline and not by impaired discharge as hypothesized, e.g. in [3]. This mechanism becomes constrained when trophic regions of ANS are exposed to interference by surrounding areas of the brain and, according to figure 1, is particularly true in small animals with correspondingly large brains because ratio of sympathicus to the whole brain decreases faster than the body weight. This can explain the potentiated increase of cancer in mice and rats and perhaps also in budgerigars, as this family has large brains.
It is appropriate to emphasize that well known neurophysiological conditions, for instance the function of the genitals, are regulated by sympathicus and parasympathicus in much the same way as may be the case with cancer. These regions, at least in humans, are subject to supervision from cortex cerebri, but in infancy the neural loops become conditioned, which will henceforth manifest as various facets of sexuality.
The concept of interference between different centers of the brain may seem abstract, but it has been established that consciously perceived events, possibly traumatic, can interfere with the functions of ANS, thereby causing sexual and hormonal dysfunction and other losses [24] [25]. The above reasoning allows the assumption that the same is true for the development of cancer.
Conclusion
Citation: Mountcastle V.B. In: Medical Physiology, 14th Edn. St. Louis: Mosby, 1980: pp. 899, 903:
- 'The autonomic unification of this system would lead one to predict a generalized discharge. This seems to be less of a mystery than the channelling of activity through this system, which permits rather discrete reflex actions and the occurrence of tonic activity in only certain of the sympathetic fibers. The centers that control this system can, to a great degree, determine whether it discharges selectively or totally. Under basal conditions, selective tonic and reflex activities occur, but under stress or in anger the system discharges as a whole'. –
References
- E.M. Taylor, A.R. Lehmann. (1998). Conservation of eukaryotic DNA repair mechanisms Int J Radiat Biol, Sep; 74(3), pp.277-86.
- P. Seifert, M. Spitznas. (2001). Tumours may be innervated Virchows Archiv, March; Volume 438, Issue 3. pp 228 – 231.
- M. Makale, S. Kesari, et al. (2017). The autonomic nervous system and cancer. Elsevier, Biocybernetics and Biomedical Engineering, May 37(3).
- Del Rey, A. Kabiersch, S. Petzoldt, H.O. Besedovsky. (2003). Sympathetic abnormalities during autoimmune processes: potential relevance of noradrenaline induced apoptosis Ann N Y Acid Sci., May pp. 992:158-67.
- E. Lundsgaard. (2003). Generalised cancer, a function of the relative brainsize Med Hypotheses. 61(2), pp. 200-5.
- D.G. Powe, M.J. Voss, H.O. Habashy, K.S. Zänker, et al. (2011). Alpha- and beta-adrenergic receptor (AR) protein expression is associated with poor clinical outcome in breast cancer: an immunohistochemical study Breast Cancer Research and Treatment, Nov Volume 130, Issue 2, pp 457–463.
- Y.C. Fu, C.S. Chi, S.C. Yin, B. Hwang, et al. (2004). Norepinephrine induces apoptosis in neonatal rat cardiomyocytes through a reactive oxygen species -TNFa-caspase signalling pathway Cardiovascular Research, June Volume 62, Issue 3, pp. 558–567.
- J.K. Dunnick, S.L. Eustis. (1991). Decreases in spontaneous tumors in rats and mice after treatment with amphetamine Toxicology, May; 67(3), pp.325-32.
- R.L.R. Snyder, H.L.R. Ratcliffe. (1966). Primary Lung Cancers in Birds and Mammals of the Philadelphia Zoo Cancer Research, March, 26, Part 1, pp. 514-518.
- Earthlife web chapters. A Bird's Brain and Nerves.
- Beluga whale, Delphinapterus leucas
- S.J. Newman, S.A. Smith Marine Mammal Neoplasia: A Review. Sage, Marine mammal neoplasia, 2006.
- W.A. Priester, G.H. Theilen, F.R. Madewell. (1979). Veterinary Cancer Medicine 1st Edn. Philadelphia. Lea and Febigir, 1979; pp. 14-32.
- S.H. Weisbroth In. (1974). The Biology of the Laboratory Rabbit 1st Edn. New York: Academic Press, pp. 261-263.
- History of the Sprague Dawley Rat
- R.E. Morrissey, S. Eustis, J.K. Hasemann, J. Huff. (1991). Huff Toxicity and Carcinogenicity Studies of Nalidixic Acid in Rodents Feb.
- Budgerigar
- H.L. Ratcliffe. (1933). Incidence and Nature of Tumors in Captive Wild Mammals and Birds Am J Cancer, 17:116-135. TABLE XII, p. 130.
- J.D. Prejean, J.C. Peckham, A.E. Casey, D.P. Grisworld, et al. (1973). Spontaneous Tumors in Sprague-Dawley Rats and Swiss Mice Cancer Research, Nov.; 33, pp. 2768-2773.
- R. Eiben. (2001). Frequency and time trends of spontaneous tumors found in B6C3F1 mice oncogenicity studies over 10 years Exp Toxic Patrol, 53: pp. 399–408. Urban & Fischer.
- L.M. Abegglen, et al. (2015). Potential Mechanisms for Cancer Resistance in Elephants and Comparative Cellular Response to DNA Damage in Humans JAMA, Nov; 314(17), pp. 1850-1860.
- Serendip Studio Measuring Brain Size versus Body-Size.
- X.Y. Huang, H.C. Wang, Z. Yuan, et al. (2012). Norepinephrine stimulates pancreatic cancer cell proliferation, migration and invasion via b-adrenergic receptor-dependent activation of P38/MAPK pathway. Hepatogastroenterology, May 59(115), pp. 889-93.
- R. Ader, D.L. Felten, N. Cohen Psychoneuroimmunology. Academic Press 1981, Book.
- S. Ranabir, K. Reetu. (2011). Stress and hormones. Indian J Endocrinol Metab. Jan-Mar; 15(1): 18–22.
Citation: Ebbe Lundsgaard. (2020). The Autonomic Nervous System Fights Cancer in Mammals and Birds. Journal of Medicine and Surgical Sciences 2(3). DOI: 10.5281/zenodo.3993834
Copyright: © 2020 Ebbe Lundsgaard. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.