Research Article
Volume 4 Issue 2 - 2022
Estimation of Coefficients of The Mathematical Model Controlling the Lactation Curve of Holstein Cows: Genetic Parameters, Correlations, Heritability and Genetic Trend
1Formerly postgraduated student
2Assistant professor, Department of Animal Science, Faculty of Agriculture, University of Tabriz, Tabriz, Iran
2Assistant professor, Department of Animal Science, Faculty of Agriculture, University of Tabriz, Tabriz, Iran
*Corresponding Author: Karim Hasanpur, Assistant professor, Department of Animal Science, Faculty of Agriculture, University of Tabriz, Tabriz, Iran.
Received: July 16, 2022; Published: October 20, 2022
Abstract
Understanding the genetic and environmental relationships which affect the lactation curve parameters can provide a wealth of information for designing breeding programs in Holstein cows. Therefore, the aim of the current study was to estimate the parameters of the lactation curve and to estimate the genetic parameters and trends in Iranian Holstein cows. To this end, 46942 first parity Holstein cows with 10 consecutive test day records were collected for genetic evaluation of the lactation curve components collected from the National Center for Breeding and Livestock Improvement during the years 2009 to 2018. Next, based on the significance of the Wood function, the parameters of this mathematical model and consequently, the genetic components, heritability and genetic trend for the Wood function parameters were estimated. Moreover, to estimate genetic parameters, univariate and multivariate analyses were performed using ASREML software. The results of the present study showed that the heritability of traits related to the lactation curve was estimated to be in the range of 0.03 to 0.27. Also, the heritability of parameters a, b and c of the Wood function is low to medium for different steps of the coefficient curve, and the share of the genetic effect is incremental in response to selection is low. One of the interesting results of this study was the similarity between the genetic trend of 305-day milk yield with the peak yield and the three stages of lactation, which shows the importance of focusing and weighting the early stage of lactation in selection. Finally, it is desirable to pay attention to the first stage of cows’ lactation in the cattle for achieving genetic improvement.
Keywords: Lactation curve parameters; Wood function; Milk yield; Holstein cows; Genetic correlation
Introduction
Because of the significance of production and composition of daily milk, the amount of milk produced at peak yield, lactation length, and lactation persistency, understanding the genetic and environmental relationships in the lactation curve seems to be an important and necessary step (Dematawewa and PJ Berger,1996). In lactating dairy cows, milk yield in three stages begins with calf calving (early lactation), and reaches its peaks after 6 to 7 weeks of calving, and finally has a declining trend up to 2 months before the next (final) calving. (Atashi et al., 2007). Understanding the curve and graphic trend of milk yield and the factors affecting it provides a wealth of information about nutritional status, management, genetics, cattle diseases, and the insemination program (Swalve and N Gengler, 1999).
If the genetic aspects of the lactation curve are determined and the mathematical models are fitted and the best model is determined, selection for the model parameters can increase the milk yield for the whole lactation period. Summary of previous studies shows that the shape of the lactation curves of different cows are very different and are highly diverse. Also, the review of previous studies shows that the lactation curve is influenced by many factors, including animal genetics, calving age, feeding, calving season, cattle production level, lactation periods, days open, breast structure, and pregnancy status (Muir et al., 2004). Understanding the lactation curve and reaching a suitable mathematical model have long been considered a breeders’ research horizon (Schmidt et al., 1988).
The importance of curve fitting functions are: producing appropriate lactation curves to study factors affecting milk yield at different stages of production (management objectives), estimating yield for missing records, correcting incomplete records to compare livestock based on a similar production period, putting parameters in the selection index in order to select for the lactation curve, the possibility of genetic evaluation of bulls before the completion of the record of all daughters. In general, mathematical models which describe the lactation curve are classified into two groups: linear and non-linear models. The mathematical models used to describe the lactation curve are mainly different in terms of linearity or non-linearity, number of parameters, time interval between sampling, sampling method, and bias. Some of these functions are: Incomplete Gamma or Wood Function (linear with three parameters), Wilmink function, modified gamma function, fixed regression model, single and multiphase function, inverse polynomial function, complex logarithmic function, exponential function, Koebe function, Rook function, and Dijkstra function.
Lactation curve models can be divided according to whether their parameters are directly related to the lactation curve traits (such as the experimental Gamma Wood function and the Pollott-Gootwine mechanistic model) or not (such as Legendre polynomial functions and fractional functions) (Macciotta et al., 2011). Among the functions presented to describe the shape of the lactation curve, the Wood function (Wood P, 1967) is one of the applied functions. Van Arendonk (Van –Arendonk JAM, 1985) used the Wood function to provide a definitive model of the dairy cow system and to estimate the performance, costs and revenues of dairy cows. Kalantari et al (Kalantari et al., 2010) used the Wood function in simulating milk yield and, in a dynamic programming model, examined the optimum replacement policy for Iranian Holstein dairy cows. A proper understanding of how milk yield changes during a lactation period can be used to determine the biological and economic efficiency of a dairy cow. In addition, by using the lactation curve, the breeder will be able to manage and breed cows based on their lactation characteristics (Adediran et al., 2007). In Iran, some cows do not have a full lactation period and are removed before genetic analysis. Therefore, when genetically analyzing bulls, removing a large number of daughters from a particular bull may lead to biased results and the animals may not be ranked properly. The summary of the results of previous research on the parameters of mathematical models controlling the lactation curve in different species indicates the appropriate contribution of additive effects and heritability of these traits, which makes it possible to change the growth curve based on genetic selection. Understanding the genetic and environmental relationships governing these parameters can provide a basis for designing breeding programs in Holstein cows.
The aim of this study was to investigate milk yield at different stages as well as in different lactation curve traits to investigate the possibility of using some lactation stages or different lactation curve traits in the selection index of dairy cows. Perhaps, it is possible to use all records (incomplete and complete) to genetically assess male breeders more accurately.
Materials and Methods
In the present study, 46942 first parity Holstein cows with 10 consecutive test day records were used. These cows had their first calving between 2009 and 2018 and their records were collected by the National Center for Breeding and Livestock Improvement in Iran. The descriptive statistics of the data used are reported in Table 1.
Mathematical functions used
The Wood function (Wood P, 1967) was employed in this study. The reason for selecting Wood function from among other functions was that in a similar study, 9 different mathematical functions were fitted for the same data, among which the most suitable function was introduced by evaluating the relevant indicators of the Wood function. Abnormal curves were identified and eliminated by the Wood function. Therefore, all curves with negative a, b or c parameters were identified as abnormal curves. The NLIN procedure of SAS software (version 9/2) was used to fit the Wood function. The statistical equation of the Wood function is as follows:
Yt = atbe-ct (1)
The Wood function (Wood P, 1967) was employed in this study. The reason for selecting Wood function from among other functions was that in a similar study, 9 different mathematical functions were fitted for the same data, among which the most suitable function was introduced by evaluating the relevant indicators of the Wood function. Abnormal curves were identified and eliminated by the Wood function. Therefore, all curves with negative a, b or c parameters were identified as abnormal curves. The NLIN procedure of SAS software (version 9/2) was used to fit the Wood function. The statistical equation of the Wood function is as follows:
Yt = atbe-ct (1)
Where yt designates the milk yield on day t, a designates a scaling factor related to the milk yield at the beginning of lactation, b designates a factor related to the slope of the increasing stage of the lactation curve, c designates the slope of the decreasing stage of the lactation curve, and e designates a constant or the Euler's number.
In addition to the components of the lactation curve, traits such as yield persistency, peak yield and peak yield day can be estimated using the Wood curve, which are estimated using equations (2), (3) and (4), respectively, as below.
In addition to the components of the lactation curve, traits such as yield persistency, peak yield and peak yield day can be estimated using the Wood curve, which are estimated using equations (2), (3) and (4), respectively, as below.
per = -(b+1) In(c) (2)
ymax = a(b/c)b e-b (3)
DIMatPeak = (b/c) (4)
Where per designates the lactation persistency, ln (c) designates a constant associated with slope of the decreasing stage of lactation, ymax designates the peak yield, a, b, and c, designate the yield function parameters, e designates a constant or the Euler’s number, and DIMatPeak designates the peak yield days.
In addition to milk yield of the whole period (yield of 305 days), milk yield in different time periods can also be estimated using the Wood function. Hence, in the present study, in addition to milk yield of 305 days, the milk yield was estimated in the first stage of lactation (first 60 days of lactation), in the middle stage of lactation (yield of 61-150 lactation days) and in the final stage of lactation (yield of 151-305 lactation days). Genetic parameters of these traits were estimated using one-tailed and two-tailed models. In two-tailed analyses, only analyses of 305-day milk yield and other traits were carried out using ASREML software (Gilmour et al., 2000). The model used was as follows.
yijkl = m + herdi + yearcj + seasck + b1 (agel-¯age) + b2 (agel -¯age )2 +eijkl (5)
Where yijkl designates the whole milk yield, m designates the population mean, herdi designates the herd effect, yearcj designates the effect of year of birth, seasck designates the effect of calving season, b1 (agel-¯age) designates the auxiliary variable of animal age at birth, b2 (agel -¯age)2 designates the auxiliary variable of the square of animal age at birth, and eijkl designates the residual effects.
To estimate genetic and phenotypic trends, the mean function of breeding values and phenotypic values from year of birth were used, respectively. In this paper, only genetic trends have been reported and phenotypic trends have been mentioned when necessary.
| Month | Mean day | Mean yield | SD |
| 1 | 14.0 | 25.9 | 6.03 |
| 2 | 44.4 | 32.4 | 6.06 |
| 3 | 74.7 | 33.1 | 5.83 |
| 4 | 105.2 | 32.8 | 5.88 |
| 5 | 135.4 | 32.0 | 5.99 |
| 6 | 165.8 | 31.1 | 6.19 |
| 7 | 196.2 | 30.1 | 6.23 |
| 8 | 226.7 | 28.9 | 6.30 |
| 9 | 257.0 | 27.6 | 6.29 |
| 10 | 287.5 | 26.0 | 6.37 |
Table 1: Descriptive statistics of data used for milk yield during the lactation period.
Results and Discussion
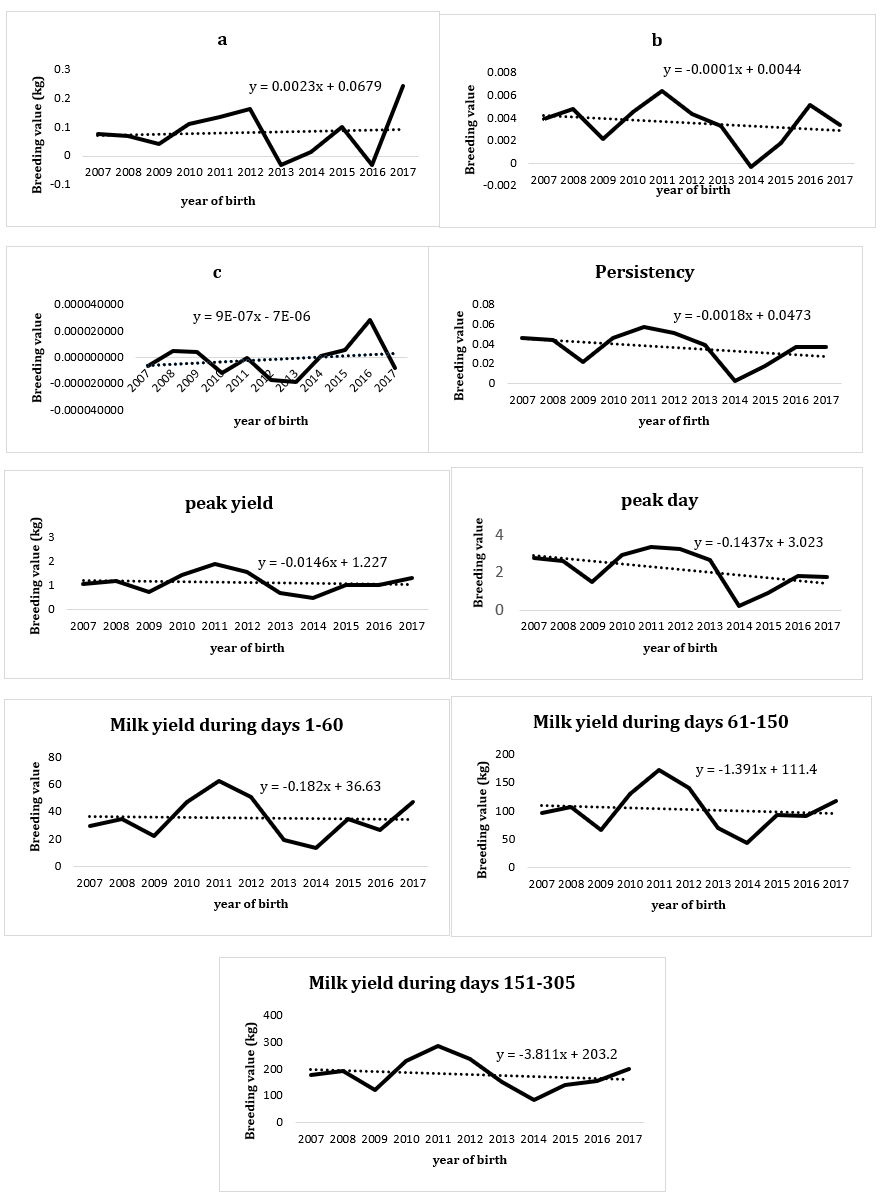
Lactation curve: Owing to the diversity of lactation curve between cows in dairy herds, it is possible to estimate the relevant genetic parameters using the coefficients of the most appropriate lactation function such as increasing and decreasing stage slopes, and to genetically select dairy cows to change the milk yield curve. The results of the current study demonstrated that the average milk yield of first parity Holstein cows had a good trend in terms of quantity and yield pattern, which reaches the peak yield (approximately 35 kg) in the second month and then with a relatively good yield persistency, it is reduced and average 25 kg yield is produced on 305 day. Figure 1 shows the milk yield curve of the first parity Holstein cows. Heritability of traits related to the lactation curve was estimated in the range of 0.03 to 0.27. These estimates were obtained from single-trait analyses. The heritability of components a, b and c of the lactation curve is very low and less than 0.05, the heritability of lactation persistency traits and peak yield day is less than 0.10 and the heritability of the first stage of milk yield (first 60 days of lactation) is estimated to be approximately 0.15. Low heritability indicates that the lactation curve is influenced by environmental-managerial factors such as appropriate climatic factors, nutrition, place sanitation and the manager's own activity in the production sector, which responds more slowly to genetic selection. Heritability, peak yield and the second and third stages of lactation with milk yield of 305 days were estimated above 0.20, which indicates that the changing the lactation curve is not easily possible and is not possible in the short term. However, selection based on 305 days of milk yield makes the same amount of genetic improvement as selection for each of the lactation stages. Figure 2 (left) shows the heritability estimated by single-trait analyses. (Hassanvand et al. (2015) estimated the heritability of milk yield persistency of Iranian Holstein cows to be 0.08. The heritability of peak yield in various studies has been estimated to be 0.1 Mikhchi et al. (2014), 0.22 Bakhtiarizadeh et al. (2010), and 0.17 Izadkhah et al. (2015). The estimated cost of milk yield depends to a large extent on the persistency of lactation, which is the rate of reduction in yield after lactation Jingar et al. (2014). For the amount of milk yield during the whole lactation period in different studies was 0.14 Strabel et al. (2004). Also, high values of heritability for these traits have been reported Shanks et al. (1980) and Sahin et al. (2012).

Figure 1: The lactation curve estimated by Wood function for the first parity; Holstein cows during 305 days of lactation period.
Genetic Parameters: Estimates of genetic and phenotypic correlations were obtained by performing two-trait analyses. Although all two-trait analyses were performed, according to the objectives of the present study, only the results of two-trait analyses between milk yield of 305 days and other traits were focused on in order to present the research idea in a better way. Genetic correlations between components a, b and c with 305-day milk yield were estimated to be moderate. Also, genetic correlations between the two traits of lactation persistency and peak time with 305-day milk yield were not very high. However, a very high genetic correlation was observed between the peak yield and 305-day milk yield, which indicates the very high impact of this trait upon milk yield during the whole lactation period. Also, a very high genetic correlation was observed between different stages of milk yield and 305-day milk yield, which is especially significant in the middle stage of lactation. Phenotypic-genetic correlations between 305-day milk yield and other traits are shown in Figure 2 (right). Although the high genetic correlation between different lactation stages with total milk yield was not unexpected, however, as will be shown below, these estimates can be promising for selection based on the cumulative yield of each lactation stage without impacting upon genetic development.
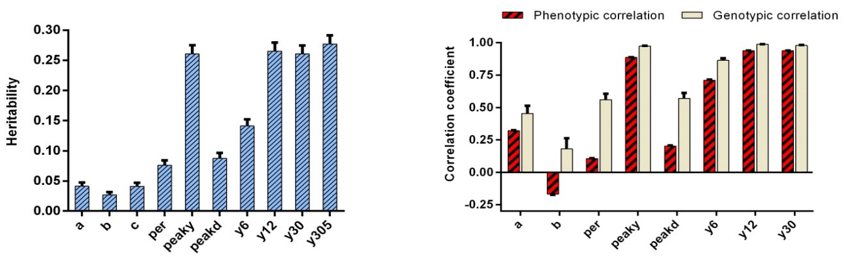
Figure 2: left: Heritability of various traits associated with the lactation curve as a single trait and right: Genetic and phenotypic correlation of different traits related to lactation curve with milk yield in 305 days.
Genetic trends of different traits associated with the lactation curve were also estimated, which are shown in Figure 3. The mean breeding value of lactation persistency decreases after 2013, so that in 2014 the values of breeding values for the genetic trend are zero and the regression coefficient of breeding values of lactation persistency is -0.0018 (p <0.01). The average breeding value of 305-day milk yield, which reached its peak in 2011, has decreased since 2012 and the regression coefficient of breeding values of 305-day milk yield is -2332/5. The trend of breeding value of yield reached its peak on the first day of lactation in 2012 and it was negative in 2013 and 2016 and the regression coefficient of yield breeding values on the first day of lactation was 0.0023. The trend of breeding value of the slope of the increasing stage of lactation reached its peak in 2011 and was negative in 2014 and its regression coefficient was -0.0001. The trend of breeding value of the slope of the decreasing stage of lactation has reached its peak in 2016. The trend of breeding value of the peak yield reached its peak in 2011 and has the lowest value in 2014. The regression coefficient of its breeding value is -0.0146. The regression coefficient of the breeding value of time to peak yield is -0.144. According to Figure3, it can be seen that the genetic trend of the lactation persistency curve with peak time is similar, which indicates that the later the peak yield of this animal occurs, the more the persistency of milk yield. The breeding value does not need to be calculated for all days, and since recording of milk production in dairy arms is very costly, it can be done based on the first 5 months of milk production instead of the entire lactation period, in which case the recording is done at a low cost. According to the study of Yazdanshenas (2002), due to the high correlation between the data collected every one month and the data collected every two months, we can reduce the number of records. Genetic trend of 305-day milk yield in studies Arshi (2014) was positive, but in the present study, the genetic trend of this trait was negative due to the high impact of the years 2011-2014. This is probably due to the small number of years studied. Because the decrease in the average breeding values during the years 2011-2014 has caused this to happen and, therefore, it can be concluded that it is better to use records of at least 20 years to estimate the genetic trend. Despite the negative genetic trend of 305-day milk yield and all three stages of milk yield, the phenotypic trend of 305-day milk yield was positive (Figure 4) and was consistent with field observations that may be due to improved managerial and environmental factors Farhangfar et al. (2007). A positive phenotypic trend has been reported for milk yield Rahmaninia et al. (2009). In addition, the phenotypic trend of milk yield and the time until the peak yield was reported to be very significant. Furthermore, Muir et al. (2004). concluded that selection to increase lactation persistency may increase total milk yield without increasing the incidence of disease or problems, and given that genetic correlation with lactation curve parameters is available, it can be considered as a good measure to improve the lactation curve. Genetic correlation between peak yield and the 305-day milk yield had the highest value among genetic correlations. Hence, increasing peak yield would be associated with increasing milk yield throughout the lactation, and if the goal is to select cows with flatter curves, this would prevent us from reaching the target.
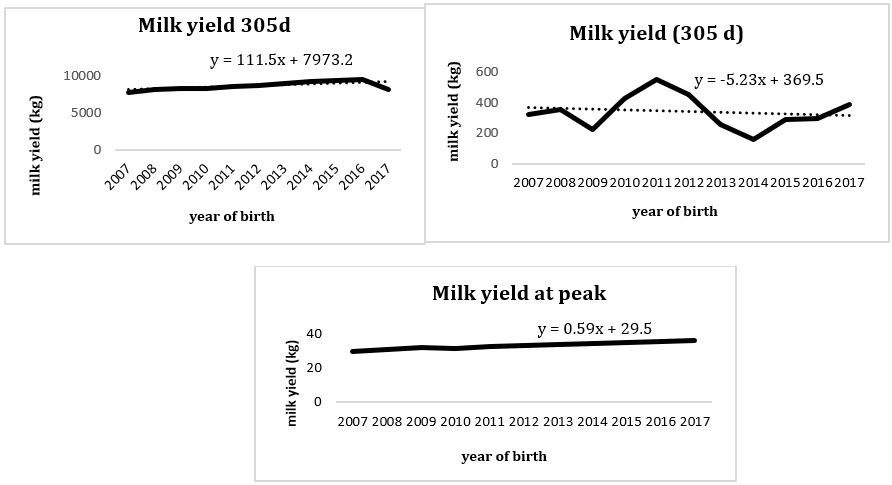
Figure 3: Phenotypic and genetic for overall milk production and 305-day lactation in Holstein cattle (first parity) Right to left respectively.
Conclusions
Using incomplete data in the genetic process is of paramount importance since there is a high correlation between milk yield at different stages with 305-day milk yield and the genetic trend of these traits is similar. It is concluded that the elimination of a large number of incomplete lactation periods of animals (cattle, buffalo or sheep) can be very biased in its selection and ranking, and it is suggested that instead of eliminating incomplete lactation periods, all animals (including animals with complete and incomplete records) be genetically evaluated with records of part of the lactation period. It is also recommended to use the record for more years. To reduce the cost of recording, instead of examining the entire lactation period, part of the lactation period (the first 5 months of the lactation period) can be recorded.
References
- Adediran, S.A; Roch, J.R; Donaghy, D.J; Rawnsley, R; Freemen, M; Nish, P; Malau-Aduli A.E.O (2007). Predictive characteristics of lactation models for pasture-based Holstein Friesian dairy cows. In: D.F. Chapman, D.A.; Clark, K.L.; Macmillan, D.P. Nation, (Editors). Dairy Journal Science. (2007). Meeting the Challenges for Pasture-Based Dairying. Proceedings of the third Australasian Dairy Science Symposium. University. Melbourne, Victoria, Australia, 3:423-430.
- Arshi A (2014). Genetic evaluation of Holstein cows of Tehran province based on 305-day milk records of first and second lactations. MSc Thesis. University. Birjand, Iran.
- Atashi, H; Moradi-shahrbabak, M; Moqimi-esfandabadi, A. (2007). Determinations of the lactation curve function in Iranian Holstein dairy cattle. Iran Agricultural Sciences Journal. 38:67-76.
- Bakhtiarizadeh, M; Moradi-Shahrbabak, M (2010). Estimation of lactation curve parameters using incomplete gamma function and their genetic association with udder type traits in Iranian Holstein cows. Iran Journal Animal Science. 21: 1-10.
- Dematawewa, C.M.B; Berger, P.J (1996). Effects of dystocia on yield, fertility, and cow losses and an economic evaluation of dystocia scores for Holsteins. Journal Dairy Science. 80: 754 .
- Farhangfar, H; Naimipur, H; Asghari, M (2007). Study of phenotypic and genetic trends of milk production traits of Iranian Holstein cows. University Birjand, Iran.
- Gilmour, AR; Cullis, BR; Welham, SJ; Thompson, R (2000). ASREML Reference manual.ftp.res.bbsrc.ac.uk in pub/aar.
- Hassanvand, S; Mehraban, H; Sadeghi Sefid Mezghi, A (2015). Estimation of genetic trend and parameters for lactation persistency of Iranian Holstein cows. Iran Journal Animl Science. 7:113-119.
- Izadkhah, R; Farhangfar, H; Fathi-Nasri, M.H (2015). Application of Wilmink’s exponential function for genetic analysis of milk peak yield and peak time of Holstein cows of Khorasan Razavi province. Iran Journal Animal Science. 1:142-150.
- Jingar, S; Mehla, R.K; Singh, M; Roy, A.K (2014). Lactation curve pattern and prediction of milk production performance in crossbred cows. Veterinary Medicine Journal Article ID 814768:1-6.
- Kalantari, A.S; Mehrabani-Yeganeh, H; Moradi, M; Sanders, A.H; De-Vries, A (2010). Determining the optimum replacement policy for Holstein dairy herds in Iran. Journal Dairy Science. 93: 2262-2270.
- Macciotta, N.P.P; Dimauro, C; Rassu, S.P.G; Steri, R; Pulina, G (2011). The mathematical description of lactation curves in dairy cattle. Itali Journal Animal Science. 10:213-223.
- MeyerK (2005). Random regression analysis using B-splines to model growth of Australian Angus cattle. Genetics, Selection and Evolution 37:473-500.
- Mikhchi, A; Hosseinpour, K; Mashhadi, M (2014). Genetic evaluation of lactation curve parameters estimated using Wilmink’s function in Holstein cows. Iran Journal Ruminant Research. 2:165-178.
- Muir, BL; Fatehi, J; Schaeffer, L.R (2004). Genetic Relationships between persistency and reproductive performance in first-lactation Canadian Holsteins. Journal Dairy Science. 87: 3029–3037.
- Rahmaninia, G; Mirzaie, H; Farhangfar, H (2009). The effect of environmental factors on the shape of the lactation curve in Iranian buffalo populations. Iran Journal Animal Science. 59-68.
- Sahin, A; Ulutas Z; Adkinson A.Y; Adkinson, R.W (2012). Genetic and environmental parameters and trends for milk production of Holstein cattle in Turkey. Itali Journal Animal Science. 11: 242-247.
- SAS Institute Inc (2004). SAS/STAT 9.1 User's Guide. Cary, NC: SAS Institute Inc.
- Schmidt, G.H; Van-Vleck L.D; Hutjens, M.F (1988). Principles of dairy science. (Second Ed.). Prentice-Hall. Englewood Cliffs, New Jersey.
- Shanks, R.D; Berger P.J; Freeman A.E; Dickinson, F.N (1980). Genetic aspects of lactation curves. Journal Dairy Science. 64: 1852-1860.
- Strabel, T; Ptak E; Szyda, J; Jamrozik, J (2004). Multiple-lactation random regression test-day model for Polish Black and White cattle. Interbull Bulletin. 32: 133-136.
- Swalve, H.H; Gengler, N; Oldham, J.D.G; Simm, A.F; Groen, B.L; Nielsen, J.E; Pryce, T.L.J; Lawrence, e.d (1999). Genetics of lactation persistency. Pages 75–82 in Metabolic Stress in Dairy Cows. BSAS occasional publication 24. British Journal Society Animal Science. Penicuik, UK.
- Van –Arendonk JAM (1985). A model to estimate the performance, revenues and costs of dairy cows under different production and price situations. Agriculture System 16: 157-189.
- Wood P (1967). Algebraic model of the lactation curve in cattle. Nature, 216:164-165.
- Yazdanshenas MS (2002). Estimation of genetic parameters of milk production traits using day test records in Iranian Holstein cows. Master of Science degree in genetics and animal breeding, faculty of Agriculture, university. Guilan, Iran.
Citation: Samaneh Khodadadi and Karim Hasanpur. (2022). Estimation of Coefficients of The Mathematical Model Controlling the Lactation Curve of Holstein Cows: Genetic Parameters, Correlations, Heritability and Genetic Trend. Archives of Veterinary and Animal Sciences 4(2).
Copyright: © 2022 Karim Hasanpur. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.